Как найти отношение закрашенной площади к не закрашенной?

Интересная задача, которая мне попалась на глаза- найти отношение закрашенной области черным к закрашенной белым. Вот у нас такая картинка:
Решение задачи соотношение закрашенных частей
1. Если мы возьмем за начало отсчета первый самый маленький квадрат, который стоит внутри – это белый квадрат, то описанный вокруг белого, первый черный квадрат относится к нашему белому квадрату как 2 к 1
Докажем это самым простым визуальным способом:
Разделим наш квадрат пополам и получим вот такую картинку, из которой мы видим, что белый квадрат состоит из 4 одинаковых треугольников, в черный квадрат состоит из одинаковых 8 треугольников 8 относится к 4, как 2 к 1. Думаю математически это не нужно доказывать!?
Из верхнего мы имеем, что площадь черного и белого равны друг другу!
У нас получится 1 единица белого и 1 единица черного…
2. Теперь, если мы проделаем это с большой картинкой. То логика сразу будет понятна!
Теперь нам нужно определить соотношение черных треугольников 2 к белым треугольникам 3, из той же логики мы видим, что они носятся к друг другу как как 8 к 4, т.е. в два раза больше, из первого пункта мы вывели, что и черных и белых по единице, если мы умножим единицу на 2, то получим 2 единицы белого
3. По той же логике мы здесь видим, что треугольник №2 относится к треугольнику №4, как 16 к 4, или 4 к 1, другими словами площадь большой площади квадрата №4 – равно 4 единицам.
Итого: 1 единица черного(№2) + 4 единицы(№4) черного = 5
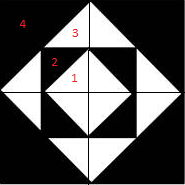
1 единица белого(№1) + 2 единицы(№3) белого = 3
Площадь черного и белого относится как 5 : 3

Написать что-нибудь...